Математика, народонаселение и великое число e

Первая перепись 

В самом конце XIX века, в 1897 году в России была проведена первая всероссийская перепись населения. Наш великий соотечественник Дмитрий Иванович Менделеев проделал огромный труд по обработке и анализу переписи. Результаты он обобщил в книге «К познанию России». Интересно отметить: в советское время это произведение Менделеева не издавалось. Теперь оно доступно каждому желающему, так как с электронной копией книги можно ознакомиться в интернете.

Основная масса населения проживала в европейской части России. Обработка данных переписи показала, что в пятидесяти губерниях, которые располагались именно в этой части, естественный прирост составлял 1,81%. Менделеев отметил, что «такого большого естественного прироста, какой найден для 1897 года в европейской России (1,81%), ни для одной страны до сих пор не известно».

В других регионах империи, включая мусульманские, темп роста населения был несколько ниже. Дмитрий Иванович полагал, что, приняв для всей страны «текущий прирост равным 1,5%», он «недалеко ушел от действительности».

Дмитрий Иванович Менделеев – великий ученый, верный и любящий сын Отечества, человек большого государственного масштаба с необыкновенно широким кругом интересов. Его единомышленниками были нобелевские лауреаты Иван Петрович Павлов и Илья Ильич Мечников, знаменитый адмирал Степан Осипович Макаров и многие другие выдающиеся современники.

Дмитрий Менделеев

Дмитрий Иванович был семнадцатым ребенком в семье. Он считал, что «высшая или гуманнейшая цель всякой «политики» яснее, проще и осязательнее всего выражается в выработке условий для размножения людского».

Действительно, если люди нравственно и физически здоровы, воодушевлены стремлением к цели, лежащей выше материальных интересов, чувствуют реальную заботу и защиту со стороны государства, то они уверенно смотрят в будущее. Такая уверенность, безусловно, способствует созданию дружных, прочных, основанных на любви больших семей, которые обеспечивают стабильный темп роста численности населения.

Неверный прогноз?

На основе темпа роста, равного 1,5% в год, Менделеев сделал прогноз динамики роста численности населения России, который принципиально разошелся с печальной реальностью. Накануне распада в Советском Союзе в 1991 году проживало 290 млн. Учитывая, что в Российской империи в 1887 году проживало 128,2 млн, и приняв темп роста равным 1,5%, можно получить, что в 1991 году могло проживать 533 млн.

Разница между прогнозом и реальностью составляет более 240 млн. Эту чудовищную величину можно назвать количественной оценкой потрясений, которые пережил наш народ в трагическом ХХ веке. Дело не в том, что Менделеев допустил ошибку, а в том, что при советской власти ситуация настолько изменилась, что стремительный рост численности населения сменился продолжительным спадом, грозящим перейти в демографическую катастрофу.

Теперь понятно, почему в СССР эту книгу Менделеева не печатали и не афишировали. В те времена ее содержание вполне могли квалифицировать как «порочащее советскую власть». Но негативные тенденции, заложенные в ХХ веке, продолжаются и усиливаются и в наше время. Дело в том, что демографические процессы обладают очень большой инерцией. Сложившиеся жизненные стереотипы невозможно изменять быстро, на это требуется значительный промежуток времени.

К сожалению, только достаточно узкий круг специалистов представляет себе реальную картину, в то время как численность нашего народа – это проблема, касающаяся всех. От благополучия или неблагополучия в этой сфере зависит наше будущее. Звучат тревожные предупреждения, но на них, можно сказать, никто не обращает внимания; раздаются голоса, вещающие, что все хорошо, все под контролем. В целом общество принимает вторую точку зрения, так как в таком случае ничего не надо делать, подтверждая правоту Пушкина, что «мы ленивы и нелюбопытны».

Жар холодных чисел

Наука, которая занимается проблемами народонаселения, называется демографией. Нам кажется, что, не претендуя на излишнюю строгость и точность, можно в общих чертах обрисовать демографические процессы, протекающие в нашей стране. Даже поверхностного взгляда достаточно, чтобы проступила динамичная, весьма драматическая, если не сказать трагическая картина.

Например, в одном учебнике по демографии для высшей школы приводится задача следующего содержания: «Если современные негативные тенденции сохранятся, то через сколько лет последний россиянин закопает предпоследнего?»

Для решения подобных задач достаточно знания школьной математики, но, к сожалению, в школьной программе решение столь актуальных задач не предусмотрено, и ожидать, что в обозримое время ситуация изменится, не приходится.

В классической древности и в средневековых университетах наряду с гуманитарными науками изучались и математические. Умение изучать количественные характеристики процессов, анализировать их, проводить некоторые расчеты являлось отражением определенного уровня культуры.

Советское образование хвалят, и справедливо. В нем было много очень хорошего, но, к сожалению, оно во многом было формальным, оторванным от практики. Коснемся преподавания математики. Появилось искусственное разделение на гуманитариев и математиков.

Если с современным человеком, получившим гуманитарное образование, заговорить о школьной математике, у него становится скучное лицо, и он перестает воспринимать совсем не потому, что у него интеллект слабый, а потому, что школьная программа напрочь отбила желание вникать в эти трудные и оторванные от жизни проблемы. Человек, способный запомнить десятки тысяч иностранных слов, выучить сотни грамматических правил, разобраться в том, что такое сложные отглагольные формы, безусловно, может разобраться и в некоторых алгебраических формулах и правилах.

Школьная программа предлагает очень трудные примеры, которые для своего решения требуют большого напряжения сил. Но, к сожалению, приложенные усилия и навыки не находят в обыденной жизни никакого практического применения, а следовательно воспринимаются как неоправданные и напрасные и, в конце концов, вырабатывают стойкое отторжение на всю жизнь.

Русский поэт Александр Блок в свое время говорил про «жар холодных чисел», но школьное преподавание математики у очень многих, если можно так сказать, своим леденящим дыханием вымораживает этот жар, оставляя только мертвящий холод.

Чтобы человек осознал реальное положение вещей, он должен иметь инструмент, который даст ему самому возможность проводить необходимые расчеты, анализировать ситуацию и принимать решения. Только в том случае, когда он сам сможет контролировать свои вычисления, он поверит полученным им результатам. В Приложении мы описываем некоторые математические приемы, которые могут быть инструментом, позволяющим самостоятельно проводить простейшие демографические расчеты.

Прирост как критерий доверия

Прирост населения является значимым критерием качества жизни народа и свидетельствует о том, насколько уверенно народ смотрит в будущее. Низкий прирост говорит, что общество в целом испытывает серьезные трудности, и нравственного, и материального порядка. Дело не в уровне жизни, а в ее качестве. Можно жить состоятельно и сознательно не иметь детей, можно их не иметь и против воли из-за нарушения здоровья. И то, и другое говорит о нарушении или нравственного, или физического здоровья народа.

Прирост населения отражает также степень доверия супругов друг другу, степень доверия в обществе в самом широком смысле, степень уверенности, что семья не останется в беде в одиночку, что есть надежные друзья и соседи, которые придут на помощь, что помощь придет и со стороны государства.

Надо задаться вопросом, что надо делать, чтобы прирост населения стал стабильно высоким, и что препятствует его росту. Это совсем не простые проблемы, и над ними надо размышлять на всех уровнях. Причем удачные решения могут быть найдены и на самом низком уровне, ведь самим родителям виднее, что им действительно необходимо для построения счастливой многодетной семьи. Конечно, надо изучать опыт отечественный и зарубежный, современный и имевший место в истории, и отбирать то лучшее, что может быть с пользой применено в современных условиях.

В семейной, да и в государственной жизни определяющими являются вера и верность. Но сейчас не стесняются публично говорить: «Брак любви не помеха». Именно такое, основанное на неверности как на норме, отношение пагубно влияет и на воспитание молодежи, и на прочность семьи, и на рождение детей, и на нравственный климат в обществе.

Стала нормой и такая порочная страсть, как сластолюбие. «И добродетель в этот жирный век / Должна просить прощенья у порока», – сказал Шекспир, тонко уловив набирающие силы тенденции, которые перестали бояться осуждения; когда в поисках чувственных утех многие готовы «валяться в сале продавленной кровати». На таких безнравственных принципах полноценной счастливой жизни не построить. Не нужно винить какие-то внешние силы в развале страны и бедственном положении народа, если фактически нравственной нормой является супружеская неверность.

В роковом 1917 году большевики бросили в народ лозунги:

Мир народам!

Власть Советам!

Земля крестьянам!

Фабрики рабочим!

Своей яркостью, простотой, понятностью и доходчивостью эти лозунги привлекли внимание народа, и какая-то его часть, поверив, откликнулась на них. Но жизнь показала, что за этими лозунгами стоял сплошной обман, а те, кто их выдвинул, стремились не к народному благу, а к захвату власти над огромной богатейшей страной. Разразилась беспощадная, кровопролитная, разрушительная гражданская война.

Часто ссылаются на слова Пушкина: «Не приведи Бог видеть русский бунт — бессмысленный и беспощадный». Но забывая про Бога, в эти слова вкладывают смысл, который, собственно, в них не содержится, а именно, что только «русский бунт — бессмысленный и беспощадный».

Подобная трактовка вызывает естественный вопрос: «А какой бунт вы хотели бы видеть: французский, американский или, например, немецкий? Потребовались колоссальные усилия и жертвы, чтобы его усмирить. Мало показалось?»

Кроме того, следующую за этими словами фразу Пушкина просто опускают, а звучит она так: «Те, которые замышляют у нас невозможные перевороты, или молоды и не знают нашего народа, или уж люди жестокосердые, коим чужая головушка полушка, да и своя шейка копейка». Это блестящая характеристика всех так называемых «пламенных революционеров» и им подобных, как бы они себя сами теперь ни именовали.

Но какая-то объединяющая идея должна быть, какие-то содержательные лозунги выдвинуть следует.

Угроза историческому существованию нашего народа надвигается с неожиданной стороны незаметно и неотвратимо. Ее источником являются в первую очередь наши собственные пороки: лень, пьянство, стяжательство, безнравственность, разобщенность, расслабленность…

Можно быть уверенным, что возвращение к тем высоким идеалам, которые на протяжении веков формировали характер русского народа, выковывали его волю, стойкость в трудных обстоятельствах, даст ему силы, как и прежде, сплотиться перед лицом общей беды и выйти из этого глубокого кризиса.

Конечно, формулировать объединяющую идею, выдвигать содержательные лозунги – не дело одного человека, тут требуются общие усилия, но мы попытаемся предложить то, что нам кажется первостепенным:

Верность Богу и Его Святой Церкви,

Верность супругов друг другу,

Готовность каждого самоотверженно, творчески и бескорыстно служить своему народу и Отечеству.

Для материального благополучия и процветания нашего народа в первую очередь необходимо его нравственное возрождение!

---

Приложение

Школьная программа дает обширный материал, но как его применять в реальной жизни, что с ним делать, не учит. Еще раз отметим, что при всех своих достоинствах школьное образование в значительной мере – схоластическое. Мы не претендуем, как решить проблему математического образования в школе. Мы рассмотрим частную задачу: как объяснить образованному, но не посвященному человеку, что такое число е.

Сначала сделаем небольшое отступление. Школьная программа приучила нас к целым числам и точным ответам. Но в реальности по-настоящему точного ничего не бывает. Например, цена килограмма мяса нам известна, а вот ровно ли килограмм у нас в руках – вопрос. Показания разных весов будут отличаться друг от друга, ведь любые измерения носят приближённый характер. При взвешивании картошки точность может быть одна, черной икры – другая, в фармацевтической или ювелирной промышленности точность должна быть очень высокой, но все равно она останется ограниченной. Все реальные измерения и вычисления имеют приближённый характер. Для наших целей вполне хватит точности в пределах 10%, то есть если вместо 1 кг наш расчет даст 0,9 или 1,1 кг, мы будем считать этот результат вполне приемлемым.

Также если у нас получится в ответе «два землекопа и две трети», то ничего особенного мы в этом не увидим. Предположим, в одной бригаде 10 человек, в другой и третьей – по 11. Сколько в среднем землекопов в одной бригаде? Всего рабочих 10+11+11=32, значит, в среднем в одной бригаде 32/3=10 и 2/3. Ничего страшного в этом нет, просто в нашей задаче на некую усредненную бригаду приходится не целое число землекопов.

Например, в демографии используется такая величина, как среднее количество детей на семью. В нашей стране на одну семью приходится в среднем 1,2 ребенка. Ясное дело, что речь идет о средних величинах, а не о реальных детях. Чтобы избежать дробных величин, можно говорить о количестве детей на 10 семей: на 10 семей приходится в среднем 12 детей. Не надо бояться дробных чисел, надо только следить, к чему они относятся. Очевидно, в конкретной семье не может быть дробного количества детей, а если речь идет об усредненных величинах – это совершенно нормально.

Нам часто придется оперировать числами, которые можно представить как сумму большого и маленького числа. Например: 10,1=10+0,1. Умножим и разделим второе слагаемое на одно и то же число, результат от этого не изменится:

10,1=10+0,1=10+0,1∙10/10.

Теперь общий множитель можно вынести за скобки, получим: 10(1+0,1/10)=10(1+0,01).

Напишем это выражение в общем виде:

a+b=a+ba/a=a(1+b/a).

Любое заданное число можно разбить на слагаемые по-разному. В наших расчетах мы будем выбирать слагаемые, ведь это полностью зависит от нашего произвола, так, чтобы их отношение не превышало 1/10, т. е. a/b<0,1. Например, 9=10-1=10(1-0,1).

Напомним одно обстоятельство. Допустим, нам надо поделить некое число, обозначим его a, в 10-й степени на это же число в 3-й степени:

a¹⁰/a³=a^10-3=a⁷.

Рассмотрим частный случай, когда степени равны

a¹⁰/a¹⁰=a^10-10=a⁰,

но a¹⁰/a¹⁰=1, так как делим число само на себя, следовательно

a⁰=1,

то есть любое число в нулевой степени равно единице.

Теперь рассмотрим простую практическую проблему: вы кладете некую сумму денег, обозначим ее m₀, в банк, например, под одну сотую текущей суммы. Введем обозначение: банковский процент обозначим p, p=1/n, в нашем случае n=100 и p=1/100. Через год вклад возрастет на m₀p рублей, то есть станет равным

m₁=m₀+ m₀p= m₀(1+p).

На следующий год вклад, равный уже m₁, возрастет уже на m₁p рублей:

m₂=m₁+m₁p= m₁(1+p).

Но m₁=m₀(1+p), тогда через два года будет

m₂= m₀(1+p)(1+p)= m₀(1+p)².

Следовательно, через произвольное число лет, обозначим его k, величина вклада составит

m_k= m₀(1+p)^k= m₀(1+1/n)^k.

Очевидно, чем больше времени вклад лежит в банке, тем сумма вклада больше.

Человеку, сделавшему вклад, конечно, важно знать, сколько денег будет у него на счету через несколько лет? Таким образом, от нас требуется умение находить численное значение выражения

(1+1/n)^k.

Параметры k и n могут быть любыми. Например, может возникнуть необходимость возвести (1+1/100) в 200-ю степень. Это, к сожалению, муторная задача, за которую и браться не хочется.

Подобная задача встала перед великими учеными еще в XVIII веке, но великий человек отличается от обыкновенного тем, что находит неожиданные подходы, которые позволяют решать трудные задачи. Ключевая идея заключается в том, что из всех имеющихся возможностей выберем только те, когда k=n, то есть нам надо найти значения выражения

(1+1/n)ⁿ

Составим таблицу

Как видим, при изменении n от 1 до 200 результат изменился от 2 до 2,71, т.е. всего лишь на 0,71. Оказывается, чем больше n, тем медленнее меняется результат. Мы сталкиваемся с поразительным фактом: с ростом n результат меняется все медленнее, приближаясь к некоторому числу, которое не зависит от n! Это утверждение можно строго доказать, но мы не будем тратить на это время и усилия. Это уникальное число обозначается буквой e.

e=(1+1/n)ⁿ (1)

Оно имеет бесконечное количество знаков после запятой. Для практических целей достаточно принять, что

e=2,71828.

Число e сравнительно легко запомнить, потому что после цифры 7 идет последовательность цифр 1828, которая совпадает с годом рождения Льва Толстого. Мы не стремимся к высокой точности, поэтому в наших расчетах мы будем считать, что

e=2,72.

Можно спросить: ну и что, что это нам дает? Ответим, уже кое-что дало: ведь при n=50 результат отличается от числа e всего лишь на 1%. Такая точность нас вполне устраивает, значит, при любом n, большем 50, мы уже знаем результат: пусть приближенно, но с точностью менее 1% он равен e.

Вернемся к нашему примеру о росте вклада в банк. Чтобы возвести 1+1/n в степень k, следует проделать простые преобразования:

(1+1/n)^k=(1+1/n)^n∙k/n=e^k/n.

Мы знаем, как возвести (1+1/100) в сотую степень. Можем возвести это число и в 200-ю степень. Покажем, как это делается.

(1+1/100)²⁰⁰=(1+1/100)^100∙2=((1+1/100)¹⁰⁰)²=e²

e²=2,72²=(2,5+0,22)²=6,25+2∙2,5∙0,22+0,0484=6,25+1,1+0,0484=7,394≈7,4

Как видим, возведение (1+1/100) в 200-ю степень свелось всего лишь к возведению e в квадрат. Это, конечно, гораздо же легче, чем умножать число 1+1/100 само на себя 200 раз.

Можем возвести (1+1/100) и в 300-ю степень, для этого надо возвести e в куб. Отметим интересное свойство числа e. Оказывается, e³ примерно равно 20.

Зная это, мы можем легко возвести e, например, в 10-ю степень:

e¹⁰=e^1+3∙3=e(e³)³= e20³=2,72∙8000=21 760.

Подобные вычисления можно проделывать в уме или используя самый простейший калькулятор.

Предположим, что нам надо извлечь из 10 корень сотой степени, т.е. возвести 10 в степень 0,01, желательно без всяких вычислительных средств. Это не такая простая задача, как может показаться на первый взгляд. А вот извлечь корень сотой степени из числа e можно без всякого труда.

Дело в том, что в формуле (1) из обеих частей равенства можно извлечь корень n-й степени:

e^1/n=((1+1/n) ⁿ)^1/n=(1+1/n) ^{n 1/n}=(1+1/n)¹=1+1/n. (2)

Подставив n=100, получим:

e^0,01=1+0,01=1,01.

Это и есть решение нашей задачи. Равенство (2) можно читать и справа налево:

1+1/n= e^1/n.

Отметим, что так же, как и любое число, e⁰=1.

Мы уже довольно много знаем о числе e. Найдем еще несколько степеней этого числа. Как мы уже отметили,

e³=20.

Найдем, чему равно e^3/2. Для этого извлечем корень из предыдущего равенства: e^3/2=20^1/2. Но корень из 20 известен с хорошей точностью 20^1/2=4,5. Это можно проверить, возведя 4,5 в квадрат. Таким образом, e^3/2=4,5.

Зная это, найдем корень из e, т.е. e^1/2:

e^1/2=e^3/2/e =4,5/2,72=4,5/(2,7+0,02)=4,5/(2,7(1+0,02/2,72))=5/(3(1+0,007))=1,667/1,007=1,65.

Теперь найдем, в какую степень надо возвести e, чтобы получить 2.

2³=8=7,4+0,6=7,4(1+0,6/7,4)= e²(1+0,08)= e^2+0,08= e^2,08

Извлечем корень третьей степени, получим

2= e^2,08/3= e^0,69.

Для ряда целей достаточно считать, что e^0,7=2.

Найдем 1/e, то есть e^-1:

e^-1=e²/e³=7,4/20=0.37

То есть число e мы можем без особого труда, пользуясь простейшим калькулятором, а в каких-то случаях обходясь и без него, возвести практически в любую степень.

Выше мы сказали, что извлечь из 10 корень сотой степени, желательно без всяких вычислительных средств, – не такая простая задача. Но теперь у нас есть инструмент, который позволит решить эту задачу без особого труда.

10=20/2=e³/e^0,7=e^3-0,7=e^2,3

10^0,01=(e^2,3)^0,01=e^0,023=1+0,023=1,023.

Составим таблицу, в которую сведем полученные нами основные результаты.

Можно вновь возразить: ведь не живет же человек 100 или 200 лет, как это связано с реальностью? На это можно ответить, что человек не живет, а народ живет.

Теперь перейдем к тому, что и послужило поводом для написания нашей работы.

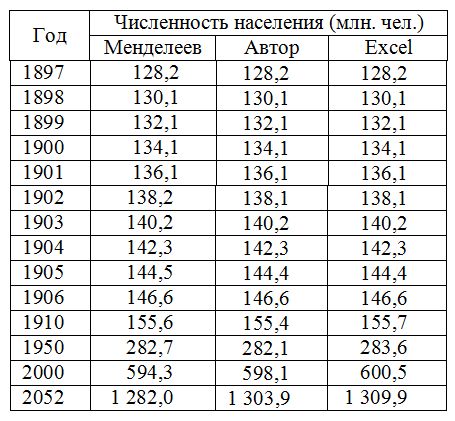
На основе темпа роста, равного 1,5% в год, Менделеев сделал прогноз динамики роста численности населения Российской империи. Мы повторили его расчеты с использованием предложенной приближенной методики, а также добавили точные расчеты по программе Excel:

Прогноз динамики роста численности населения Российской империи 

Прирост населения равен произведению темпа роста на численность населения. Чтобы получить численность в данном году, надо к численности предыдущего года прибавить прирост за год, например:

128,2+0,015∙128,2=128,2+1,9=130,1

Для расчета численности в интервале с 1897 по 1906 гг. будем использовать подобные соотношения. Как видим, в этом интервале результаты расчетов совпадают.

Численность населения в 1910 г. найдем из соотношения:

146,6 e^0,015∙4=146,6 e^0,06=146,6(1+0,06)=155,4.

Численность населения в 1950 г. найдем, используя предыдущий результат:

155,4e^0,015∙40=155,4e^0,6=155,4e^0,5+0,1=155,4∙1,65∙1,1=282,1.

Численность населения в 2000 г.

282,1e^0,015∙50=282,1e^0,75=282,1e^0,69+0,06=282,1∙2(1+0,06)=564,2(1+0,06)=564,2+33,9=598,1.

Численность населения в 2052 г. найдем, зная численность в 2000 г.

598,1e^0,015∙52=598,1e^0,78=598,1e^0.69+0,09=598,1∙2(1+0,09)=(1 200-3,8)(1+0,09)=1 200-3,8+108-0,3=1 303,9.

Как видим, предложенный способ дает результаты, отличающиеся от точных, полученных по программе Excel, не более чем на 1% и не уступающие точности расчетов Менделеева.

Аналогично найдем численность населения, которая могла бы быть в 2015 г.

598,1e^0,015∙15=598,1e^0,225=598,1(e^0.075)³=598,1(1+0,075)³=598,1∙1,242=742,8.

Согласно расчетам Менделеева к 2052 году численность населения Российской империи должна была вырасти в десять раз по отношению к 1897 году и достичь 1 млрд 282 млн человек, то есть практически сравняться с населением современного Китая. «Тогда всей земли на душу придется в России полторы десятины, а годной для земледелия — около одной десятины, т. е. больше того, что теперь имеют англичане, китайцы и т. п. Это добро надо сохранять уже ради одной любви к детям» [1], – завещал ученый. Это было бы государство с колоссальным духовным, экономическим, научным и культурным потенциалом.

В 1950 году население СССР по данным официальной статистики составило 178,5 млн человек. По прогнозам Менделеева можно было ожидать 282,7 млн человек. Правда, территория Российской империи несколько превышала территорию СССР, поэтому в границах СССР можно было бы ожидать 260-270 млн человек. Таким образом, уже к 1950 г. демографические потери составили около 85 млн человек. Они вызваны Первой и Второй мировыми войнами, гражданской войной, голодом 20-х и 30-х годов ХХ века, раскулачиванием, коллективизацией, репрессиями. Это говорит о том, что не всем было так уж «хорошо в стране советской жить».

Но даже Первая мировая и гражданская война, революция и голод не могли подорвать высокую рождаемость, унаследованную с дореволюционных времен. Было зафиксировано, что в СССР в 1926 г. проживало 147,0 млн человек, родилось 6,38 млн, умерло 3,04 млн, прирост составил 3,34 млн, темп роста – отношение прироста к текущей численности 3,34/147,0=0,0227. Мы можем посчитать, сколько жителей было бы в довоенных границах, например, в 2014 году:

147,0e^0,0227∙88=147,0e²=147,0∙7,4=1 084 млн.

В 20-х годах ХХ века еще сохранялся крестьянский уклад жизни, если бы он не был разрушен, то в стране было бы более миллиарда жителей.

Мы продемонстрировали, как любой человек может самостоятельно провести расчеты народонаселения нашей страны и самостоятельно убедиться, какова цена революции и правления большевиков. Нам кажется, что описанный математический аппарат дает в руки любому человеку инструмент, с помощью которого можно проводить расчеты, контролируя каждый свой шаг и не позволяя недобросовестным СМИ, делающим сенсации, основанные на недостоверной статистике, морочить себе голову.

Мы сравнили текущую ситуацию с той, которая была бы возможной, если бы не потрясения, постигшие Россию. Сравним с ситуацией, которая сложилась в современности.

В африканской стране Уганда в настоящее время проживает 33 миллиона человек. В этой стране рождаемость такая же, как в России до революции – 48 человек на 1000 жителей, а смертность почти в три раза меньше – 12 на 1000, следовательно, темп роста населения исключительно высок и составляет 36 на 1000 жителей. Имея описанный математический аппарат, мы можем рассчитывать количество населения через произвольное количество лет. Возьмем интервал времени, равный ста годам. Таким образом, нам надо решить задачу:

33e ^0,036∙100=33e ^3,6=33e ^3+0,5+0,1=33e³e ^0,5e ^0,1.

Мы знаем, что e ³=20, e ^0,5=1,65, e ^0,1=1+0,1=1,1.

Тогда

e³e ^0,5e^0,1=20∙1,65∙1,1=33∙1,1=36,3.

Таким образом, за сто лет население Уганды вырастет более чем в 36 раз, и в ней будет проживать 33∙36,3=1 200 млн человек! За это же время население России составит 87 млн. Если сейчас население нашей страны более, чем на 100 млн превосходит население Уганды, то через сто лет население Уганды более чем на миллиард будет превосходить население нашей страны.

Сто лет – это, конечно, очень большой промежуток времени. Давайте узнаем, через сколько лет население России и Уганды сравняются? Нам надо решить уравнение

143e ^-0,005t=33e ^0,036t

Числовые множители справа и слева от знака равенства можно сократить на 11.

13/3=e^{0,036t +0,005t}=e^0,041t

(13,5-0,5)/3=(4,5-0,5/3)=4,5(1-0,5/(4,5 3))=e^1,5(1-1/27)= e^1,5-1/27= e^1,5-0,037=e^1,463.

Итак, e^1,463=e^0,041t, следовательно, степени равны

1,463=0,041t и t=1,463/0,041=35,7 лет.

Следовательно, примерно через 36 лет численность наших стран будет одинаковой и составит

33e^0,036∙35,7=33e^1,285.

Найдем, чему равно e^1,285.

e^1,285= e e^0,3-0,015= e e^1-0,7 e ^-0,015=e²(1-0,015)/e^0,7=7,4(1-0,015)/2=3,7(1-0,015)=3,64.

Тогда

33e^1,285=33∙3,64=120 млн чел.

За 36 предстоящих лет население Уганды возрастет почти в четыре раза, а население нашей страны без войн и революций сократится на 23 млн человек. В то же время население ряда африканских, азиатских, южно-американских стран будет стремительно расти. Если ничего не предпринимать, то с течением времени численность населения нашей страны будет неуклонно снижаться.

Текущее положение с воспроизводством населения в нашей стране очень неблагополучное, если не сказать катастрофическое. Необходима конструктивная реакция всего народа для того, чтобы найти выход из этой грозящей крахом ситуации.

[1] Д.И. Менделеев. К познанию России. М. Айрис пресс. 2002 г. с 43.

---

Читайте также:

• Чьей будет Россия через сто лет?
• Демографические потрясения в России: О заводах на крови и переполненной Москве
• Протоиерей Александр Ильяшенко: Что же делать с абортами в России? (+Видео)